You are viewing an old version of this page. View the current version.

Compare with Current View Page History

« Previous Version 37 Next »

Introduction

The EWA Algorithm for swath data projection is a highly efficient and well-established approach for projecting Earth-Observational swath data to a “regular" grid.  It likely also has some possible “off-label” applications to projecting geographically gridded data and general data regridding - without reprojection (shifting grid alignment and changing resolution). Another possible application would be to general reprojection of projected data grids.

History and Relevancy

  • EWA was developed at NSIDC for MODIS swath data handling, circa 1990’s. Originally developed (and still available) as part of MODIS Swath-to-Grid Toolbox (MS2GT)
  • It is designed and capable of handling swath data with multiple rows per scan, containing data points “across-track” per scan and with rows being “along-track" to the satellite or aircraft path. Such data can exhibit the so-called “bow-tie” effect where the sample-spot (data cell) reflects an increasing area away from the nadir observation directly below the satellite.  This includes side to side angular stretching, as well as some forwards and backwards stretching across multiple scan-rows of data.  These angular perspectives create an elliptical stretch of the sample-spot away from the center of the scan.
    • The original IEEE article includes a diagram showing the elliptical source cell to target cell mapping (shown left to right below).  This corresponds to the stretching of the data acquisition sample spot when off-nadir to the satellite instrument.

Comparison of swath projection and grid reprojection

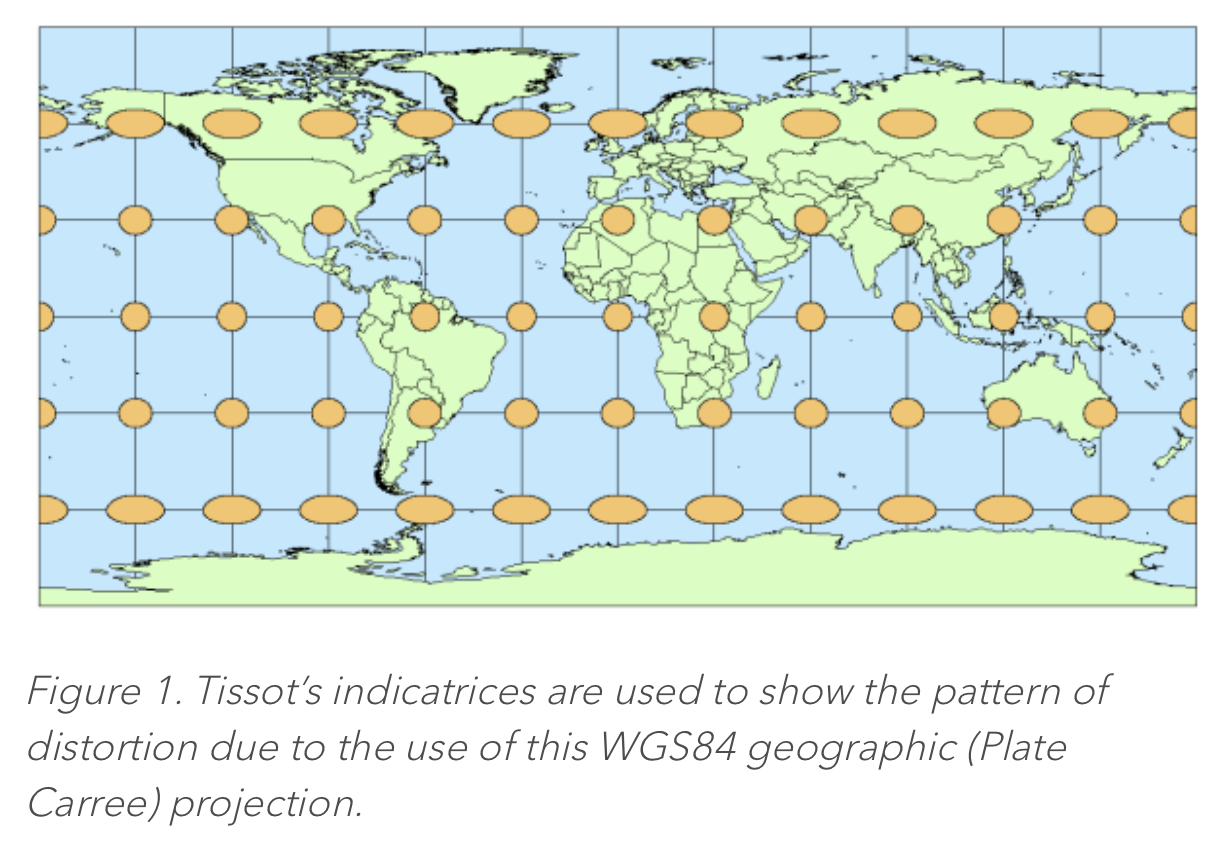
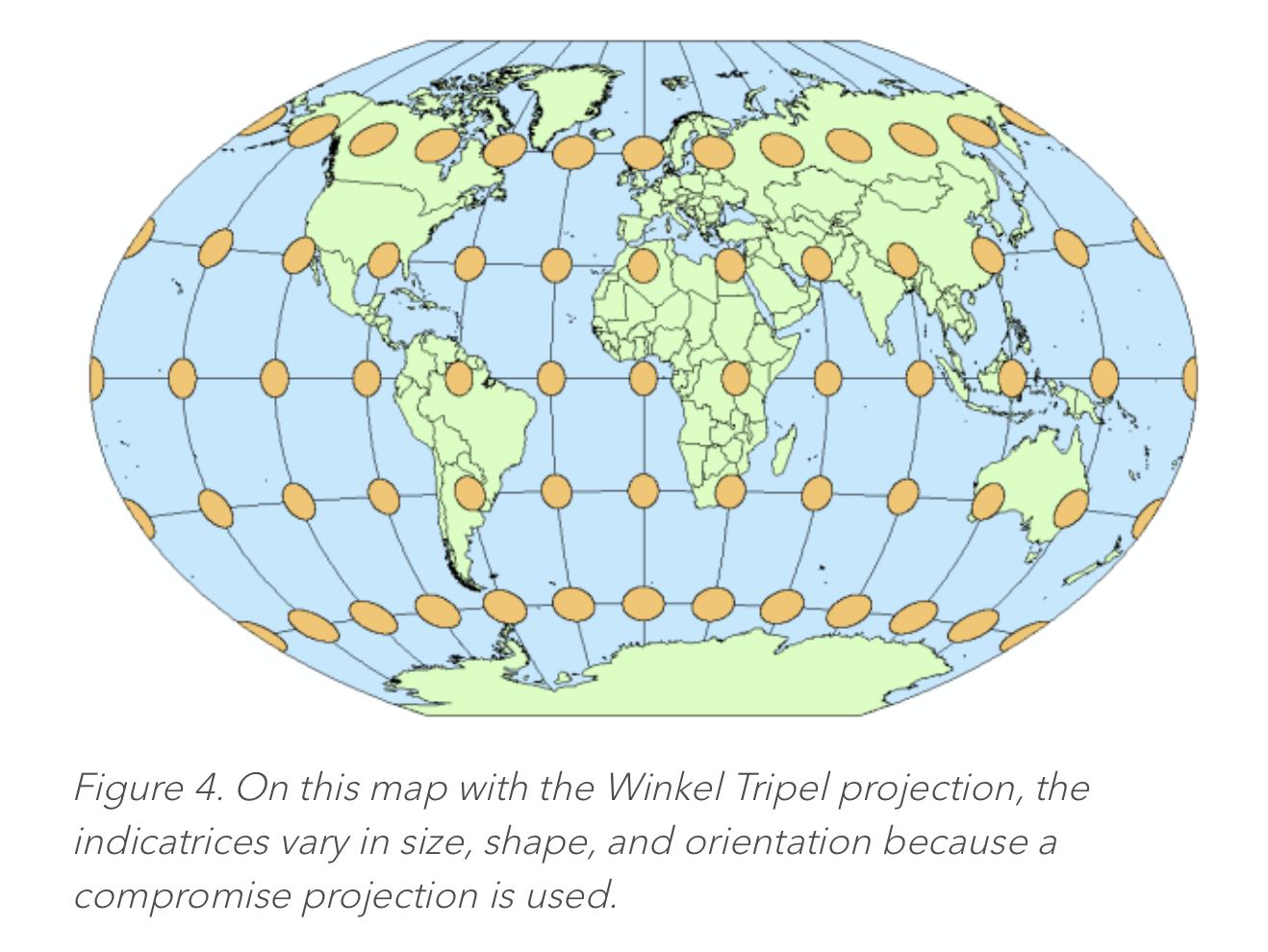
  • Note that the elliptical perspective of the EWA algorithm for swath data is quite similar to the Tissot Indicatrix ellipse of earth-data-to-flat-map projections – which shows the east-west and north-south angular distortion of a projection. There will be more discussion on this later in “off-label” applications of the EWA algorithm.  [Application of EWA for grids would not involve multiple rows-per-scan of swath data acquisition, rather referring to just one row of projected data per step through the rows (rows-per-scan = 1)].
  • In fact, even within the EWA algorithm, there is the elliptical area of the "sample-spot", and there is a Tissot ellipse of projection stretch (distortion) of the sample spot to a flat-earth grid.  The algorithm does not particularly focus on these two sources of elliptical coverage separately, but simply computes an ellipse of coverage from the source data to the target grid.
    • This article provides a good introduction to Tissot's Indicatrix: https://www.esri.com/arcgis-blog/products/product/mapping/tissots-indicatrix-helps-illustrate-map-projection-distortion/

    • The orange ellipsoids above represent a “unit perimeter/sweep of the scale-factor vector” at each selected point. Tissot’s work proved that the shape of the unit perimeter was always an ellipse.  I believe also that there is always a quadratic mapping between the ellipses at corresponding points in the two projections – another, but different “ellipse of influence” between the source and target grids.  This is what the EWA algorithm uses – the unit perimeter of scale-factor as an “area of influence” from a source data point to the target projection. It computes the parameters for an ellipse in the target projection, based upon cell delta mapping/location values between the source and target grids.

    • For forwards projection, the source data is processed forwards to the target grid by calculating the target projected location and “ellipse of influence” for each source cell.  At the end, each target cell has potentially multiple source cells that map to the target cell.  The algorithm calculates a weighted average of all source cells that map to a given target cell.  It calculates during the processing of source data points, the target points of reference, the weighted-values accumulated as the numerator, and the weights themselves summed as the denominator.  After the source data is processed, the end results is the quotient of numerator to denominator values per target grid cell.

Overview and Discussion

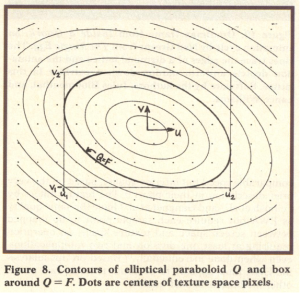
  • At its core, the EWA algorithm looks at the cell-to-cell delta in source to target cell mapping, both along and across track. These deltas are used to compute the parameters for a quadratic equation defining an “ellipse of influence” from a source cell to one or more target cells.
  • The “ellipse of influence” is used both to compute which target cells are affected by a source cell – a bounding box to the ellipse of influence – and to compute a weighting factor for a weighted averaging of source cells per target cell. The weighting is defined in terms of the distance of the source cell center location to the target cell center (radius of the ellipse).  Those source cells closer to the target cell are weighted more heavily than a simple linear cell-to-cell distance.

  • The “ellipse of influence” provides an important technique for calculating the area of influence, in the target grid.  It is an efficient way of finding target cells when forward projecting the source data grid to the output grid. This permits a reasonably efficient “forward navigation” approach, versus more typical reverse projection algorithms.

Anti-aliasing Filter

  • An important but not always evident aspect of the EWA algorithm is a further adjustment of the weighting factors to implement a gaussian filter to the projection processing. The gaussian filter is important to minimizing the possible aliasing and moiré effects when down-sampling a larger array of source data to a smaller set of target data.
    • The topic of aliasing and moiré effects in digital image processing is complex. In brief, and perhaps unsatisfyingly so, anytime you digitize at a specific resolution, or "down-sample" from a higher resolution to lower resolution, it is possible to introduce patterns of imaging that suggest lines or curves that are not present in the original or source image.
    • Here is one article that describes the effect, both in terms of audio sampling (where I first encountered this) and in video sampling:  https://matthews.sites.wfu.edu/misc/DigPhotog/alias/index.html.  (That is from a physics professor at Wake-Forest U., in North Carolina.  An interesting site, and not a bad explanation of what is happening).
    • There is another article that correlates the frequency domain analysis and the various discrete filtering techniques in image processing, suggesting further that the gaussian filter used in EWA is an important if not perfect mechanism to reducing aliasing and moire patterns.  I can’t claim to fully understand this, but it does correlate the image processing world with our reprojection efforts.  Note that wherever the reprojection mapping of source data to target projection results in “downsampling” of an input area to an output area - aliasing can occur if some kind of interpolation filtering is not applied.  This is not uniform across the output dataset, as reprojection itself is not uniform, but very often applies in some area of the output: https://www.strollswithmydog.com/downsizing-algorithms-effects-on-resolution/#more-954.
    • I’m reminded that HEG chooses a higher output resolution that minimizes downsampling effects (eliminates?), while GDAL chooses an output resolution that preserves overall grid sizing, generally at a lesser resolution, and that can introduce downsampling artifacts.  While HEG's approach may not eliminate the issue (TBD), it certainly does minimize the issue somewhat.

The algorithm itself

What follows is a very cursory pseudo-code description of the algorithm, hopefully highlighting the important aspects, and not leaving out any significant details, while not overwhelming with detail.

For each point in swath (per row, per column)
  Pre-Calculate ll2rc – lat/lon-to-row-column
  (giving floating-point row/col in target space, not integer row/col) 
For each row-set in swath (rows-per-swath)
  Compute_ewa_parameters: (ellipse parameters per column)
    For each column in swath
      <compute ellipse parameters>
        Use values in adjacent columns for horizontal delta of ellipse calculation
        Use first row of row-set to last row of row-set, averaged over the number of rows
          for the vertical delta of ellipse calculation.
  Compute_ewa: (output values per target grid cell)
    For each row in row-set
      For each column in swath
        <assign values for recurring factors >
        <get ewa_parameters for row & column (ewa_parameters, ellipse)
        <compute perimeter box for ellipse >
        For each target row in perimeter box
          For each target column in perimeter box
          If target point within ellipse
            Compute/Lookup weighting factor
            Numerator_array(target_cell)    += weighted-distance # grid_accums
            Denomitnator_array(target_cell) += weights           # grid_weights
Target_Values = Numerator_array / Denominator_array              # output_grid

The original article shows the calculation of the perimeter-box for the ellipse as follows:

EWA Performance

  • EWA should provide relatively good performance, relative to other reprojection techniques, though it remains computationally intensive to perform projection math on every point in the source grid.
  • The PyResample implementation offers a built-in DASK application that should improve performance across multi-core/multi-processor systems, without requiring a huge memory footprint.
    • EWA is an example of forward reprojection, where the source data grid is processed per cell, and with each mapping to 1 or more target cells to be processed.
    • Computationally, the biggest factor is performing the complex projection math for each source cell.
    • The processing is O(n * m)  - where n is the number of source points and m is the average size (number of cells) of the mapped bounding ellipse, typically < 24 and usually closer to 4 or 6. You may call the upper bounds on the size of m an educated guess, but it has been borne out in practice. 
    • The heavy lifting of computing the projection space of the source data (ll2rc) is O(n).  This is typically done once and reused for multiple science data variables per file.
    • In comparison, reverse projection algorithms have a similar O(n * m) load, where n is the number of target points, and m is the mapping factor to source data cells.  Also involved is an O(n * log-n) lookup factor to find related source cells.  Typically the source cells are preprocessed into an easily searched data structure (PyResample uses a K-dimension Binary Tree - KD-Tree).  The preprocessing includes the reprojection math and the results can be reused for multiple science data variables per file.
    • The two reprojection approaches likely have similar O() factors, but the additional complexity of the data structures and data search in reverse reprojection results in somewhat slower performance.
    • We noted this on the implementation of the Swath-Projector application.  EWA was similar to the other reprojection options (reverse reprojection), but generally always the faster choice.

“Off-label” application of EWA

  • Application to Geographically Gridded data, to regridding of data without reprojection, and to general reprojection of projection-gridded data
  • The impact of the rows-per-swath parameter and options of rows-per-swath = 1 and rows-per-swath = 0 => all rows … .
  • New modules to replace ll2rc – lldim2rc (Geographic Grids), rc2rc (Regridding, no projection math), xy2rc (Projected Grids, Double projection, Source-to-Target)
  • Application to Geographically Gridded data
      • There is a relatively direct relevancy of the EWA algorithm to the reprojection of geographically gridded data.  
      • The application of EWA in this case appears valid from a reprojection perspective.
        • For geographically gridded data we have an array of data, with correlated latitude and longitude values.  It is easy to see how the algorithm would be applied.  
        • When you look at a geographically gridded data array versus a swath data array, you can see that the geographically gridded data is generally wider than the swath, but there is no elliptical stretching of the grid cells in their geographic spacing.  The ellipse of influence for the source data is circular.  
        • There remains, however, the non-circular ellipses of influence due to the reprojection to a non-geographic, projected grid.  This is properly handled by the EWA implementation.
      • EWA should be a relatively efficient implementation relative to reverse projection techniques.
        • The source-cell to target-cells mapping does not have the elliptical spread of the sample-spots to consider - only the elliptical spread of the projection mapping.  There should be no more, and likely fewer cells per source cell, and thus greater efficiency per source cell count than for a swath dataset.
      • The algorithm has a gaussian filter built-in to mitigate down-sampling aliasing effects, where relevant in the output projected grid.
      • In this case, the preprocessing step of EWA - the Latitude-Longitude-to-Row-Column calculation (ll2rc) can be handled in one of two ways
        • The latitude/longitude arrays of values can be precomputed (if not directly available) and then fed into the ll2rc method
        • Alternatively, the ll2rc method can be modified into a method that directly uses the 1D dimension-scales (dimension-variables) providing latitude and longitude values.  I would call such a method llDim2rc.

  • Application to Regridding - without reprojection

      • This is a curious and perhaps less clear "off-label" application of the EWA algorithm
      • In this case the mapping of source cells to target cells is exactly circular, not elliptical.  Note however, that the EWA approach of looking at location-mapping deltas between adjacent row and column data still results in an appropriately defined "circle of influence" between the source and target grids.
      • Note also that this particular application of EWA does not care if the source/target arrays are geographically gridded or projection gridded - only that the source and target grids have the same projection.
      • Again the ll2rc method has some special handling considerations
        • There is nothing preventing the use of the first approach outlined above for application to reprojecting Geographically Gridded data - excepting for the inefficiency and processing time required.
          • I refer here to computing a pair of lat/lon datasets that can be fed into ll2rc to compute the mapping between source cells and target cells.
          • This requires projecting the source cell locations to lat/lon, and then projecting that back to the target cell locations.
          • As noted, ll2rc will work in this way but the double projection math involved is significant and ultimately unnecessary
        • Alternatively, the ll2rc method can be replaced with a method to compute the relative locations of the source and target cells using the two grid definitions and without consideration of the grid-projection involved.  This can be done producing the same data results as the ll2rc method - a source to target mapping of row-column values, floating point results, i.e., to the target row-column space.
          • I refer in this case to the grid definition as the combination of x and y projected locations of the corner points, in projected meters (or lat/lon for geographic grids); the number of rows and columns; and implicitly, the cell resolution in projected meters (degrees for geographic grids).
          • Reprojection math can be replaced with affine-matrix math, as one approach
          • I would call such a method rc2rc.
  • Application to General Reprojection


  • No labels