Introduction

The EWA Algorithm for swath data projection is a highly efficient and well-established approach for projecting Earth-Observational swath data to a “regular" grid.  It likely also has some possible “off-label” applications to projecting geographically gridded data and general data regridding - without reprojection (shifting grid alignment and changing resolution). Another possible application would be to general reprojection of projected data grids.

History and Relevancy

  • EWA was developed at NSIDC for MODIS swath data handling, circa 1990’s. Originally developed (and still available) as part of MODIS Swath-to-Grid Toolbox (MS2GT)
  • It is designed and capable of handling swath data with multiple rows per scan, containing data points “across-track” per scan and with rows being “along-track" to the satellite or aircraft path. Such data can exhibit the so-called “bow-tie” effect where the sample-spot (data cell) reflects an increasing area away from the nadir observation directly below the satellite.  This includes side to side angular stretching, as well as some forwards and backwards stretching across multiple scan-rows of data.  These angular perspectives create an elliptical stretch of the sample-spot away from the center of the scan.
    • The original IEEE article includes a diagram showing the elliptical source cell to target cell mapping (shown left to right below).  This corresponds to the stretching of the data acquisition sample spot when off-nadir to the satellite instrument.

Comparison of swath projection and grid reprojection

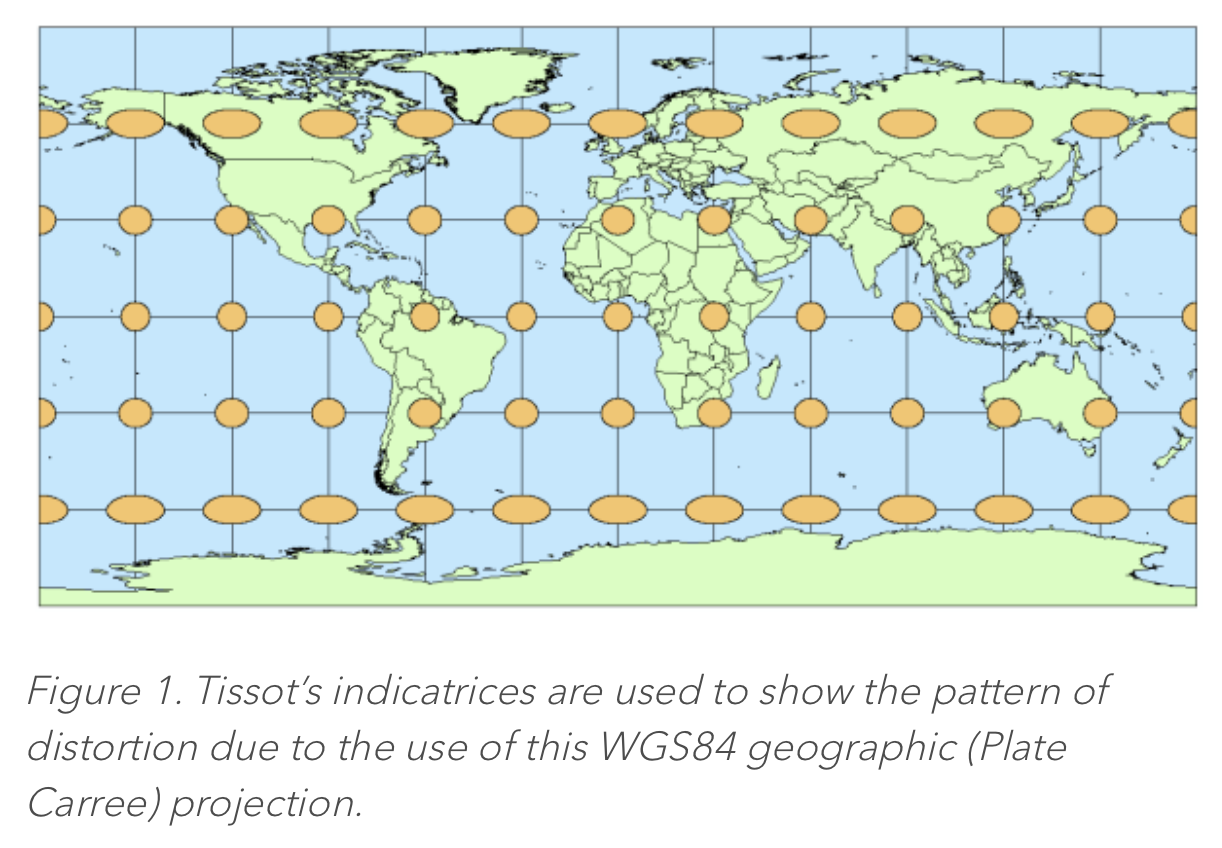
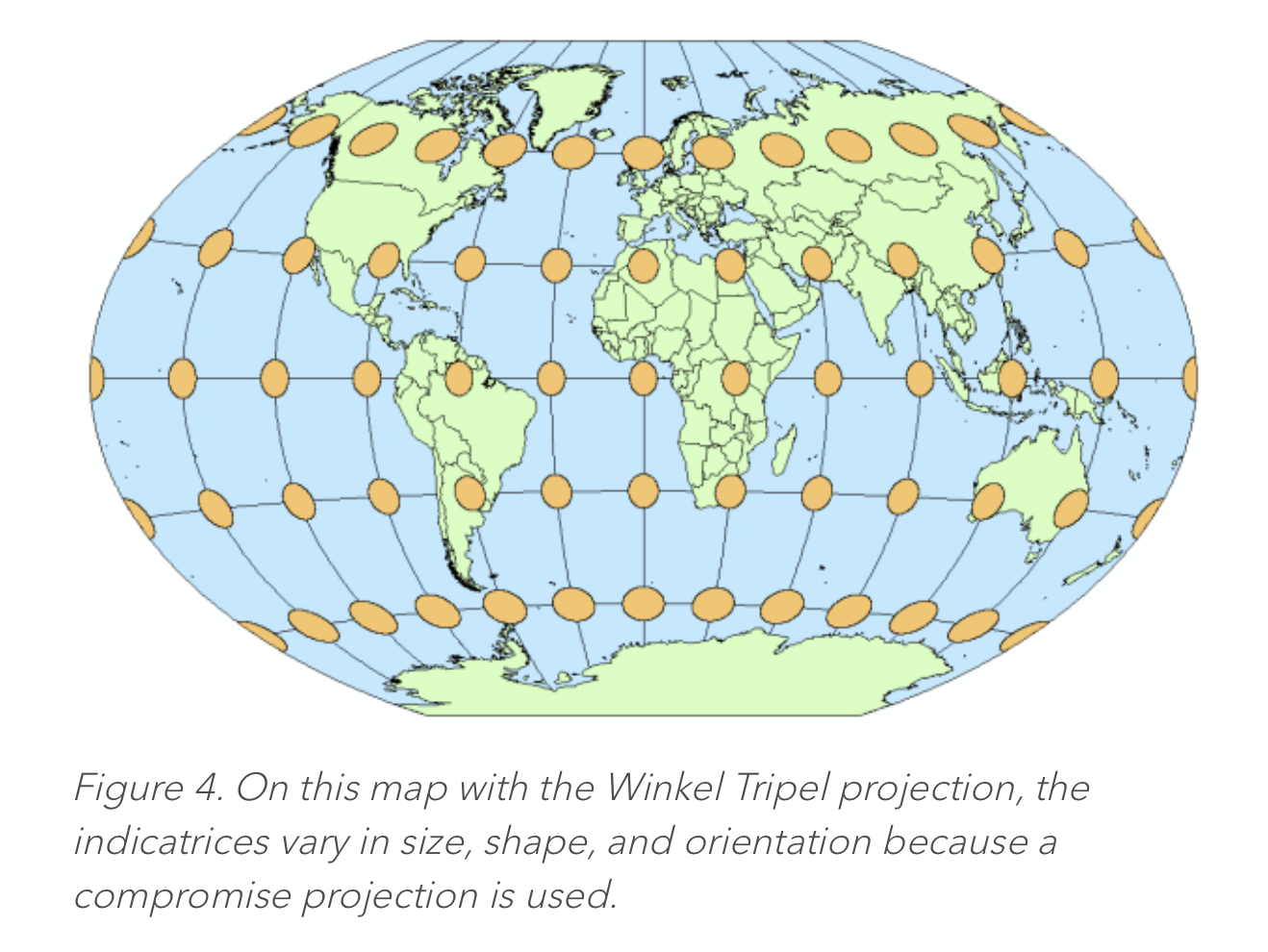
  • Note that the elliptical perspective of the EWA algorithm for swath data is quite similar to the Tissot Indicatrix ellipse of earth-data-to-flat-map projections – which shows the east-west and north-south angular distortion of a projection. There will be more discussion on this later in “off-label” applications of the EWA algorithm.  [Application of EWA for grids would not involve multiple rows-per-scan of swath data acquisition, rather referring to just one row of projected data per step through the rows (rows-per-scan = 1)].
  • In fact, even within the EWA algorithm, there is the elliptical area of the "sample-spot", and there is a Tissot ellipse of projection stretch (distortion) of the sample spot to a flat-earth grid.  The algorithm does not particularly focus on these two sources of elliptical coverage separately, but simply computes an ellipse of coverage from the source data to the target grid.
    • This article provides a good introduction to Tissot's Indicatrix: https://www.esri.com/arcgis-blog/products/product/mapping/tissots-indicatrix-helps-illustrate-map-projection-distortion/

    • The orange ellipsoids above represent a “unit perimeter/sweep of the scale-factor vector” at each selected point. Tissot’s work proved that the shape of the unit perimeter was always an ellipse.  I believe also that there is always a quadratic mapping between the ellipses at corresponding points in the two projections – another, but different “ellipse of influence” between the source and target grids.  This is what the EWA algorithm uses – the unit perimeter of scale-factor as an “area of influence” from a source data point to the target projection. It computes the parameters for an ellipse in the target projection, based upon cell delta mapping/location values between the source and target grids.

Overview and Discussion

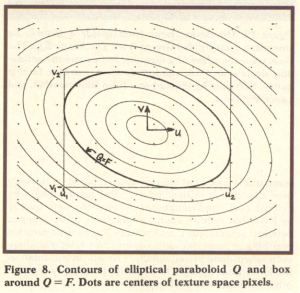
  • At its core, the EWA algorithm looks at the cell-to-cell delta in source to target cell mapping, both along and across track. These deltas are used to compute the parameters for a quadratic equation defining an “ellipse of influence” from a source cell to one or more target cells.
  • The “ellipse of influence” is used both to compute which target cells are affected by a source cell – a bounding box to the ellipse of influence – and to compute a weighting factor for a weighted averaging of source cells per target cell. The weighting is defined in terms of the distance of the source cell center location to the target cell center (radius of the ellipse).  Those source cells closer to the target cell are weighted more heavily than a simple linear cell-to-cell distance.

  • The “ellipse of influence” provides an important technique for calculating the area of influence, in the target grid.  It is an efficient way of finding target cells when forward projecting the source data grid to the output grid. This permits a reasonably efficient “forward navigation” approach, versus more typical reverse projection algorithms.

  • For forwards projection, the source data is processed forwards to the target grid by calculating the target projected location and “ellipse of influence” for each source cell.  At the end, each target cell has potentially multiple source cells that map to the target cell.  The algorithm calculates a weighted average of all source cells that map to a given target cell.  
  • It calculates - during the processing of source data points - the target points of reference, the weighted-values accumulated as the numerator, and the weights themselves summed as the denominator.  After the source data is processed, the end result is the quotient of numerator to denominator values per target grid cell.
  • This technique allows a single pass through the source data grid - to both identify the target cells and compute a partial solution to the output value - the numerator and denominator values.  This is followed by a simple pass through the target cells to divide the numerator (weighted sum of values) by the denominator (sum of weights).

Anti-aliasing Filter

  • An important but not always evident aspect of the EWA algorithm is a further adjustment of the weighting factors to implement a gaussian filter to the projection processing. The gaussian filter is important to minimizing the possible aliasing and moiré effects when down-sampling a larger array of source data to a smaller set of target data.
    • The topic of aliasing and moiré effects in digital image processing is complex. In brief, and perhaps unsatisfyingly so, anytime you digitize at a specific resolution, or "down-sample" from a higher resolution to lower resolution, it is possible to introduce patterns of imaging that suggest lines or curves that are not present in the original or source image.
    • Here is one article that describes the effect, both in terms of audio sampling (where I first encountered this) and in video sampling:  https://matthews.sites.wfu.edu/misc/DigPhotog/alias/index.html.  (That is from a physics professor at Wake-Forest U., in North Carolina.  An interesting site, and not a bad explanation of what is happening).
    • There is another article that correlates the frequency domain analysis and the various discrete filtering techniques in image processing, suggesting further that the gaussian filter used in EWA is an important if not perfect mechanism to reducing aliasing and moire patterns.  I can’t claim to fully understand this, but it does appear to again correlate the image processing world with our reprojection efforts.  https://www.strollswithmydog.com/downsizing-algorithms-effects-on-resolution/#more-954. 
    • Note that wherever the reprojection mapping of source data to target projection results in “downsampling” of an input area to an output area - aliasing can occur if some kind of interpolation filtering is not applied.  This is not uniform across the output dataset, as reprojection itself is not uniform, but very often applies in some area of the output.
    • I’m reminded that HEG chooses a higher output resolution that minimizes downsampling effects (eliminates?), while GDAL chooses an output resolution that preserves overall grid sizing, generally at a lesser resolution, and that can introduce downsampling artifacts.  While HEG's approach may not eliminate the issue (TBD), it certainly seems to minimize the issue somewhat.
    • Subjectively I'll note that aliasing and moiré effects have been very visible in previous reprojection efforts.  In the development of the Swath-Projector application both forward (EWA) and reverse (nearest-neighbor, bi-linear) projection/interpolation options were implemented. Very often the nearest-neighbor and bi-linear (without filters) introduced these effects, along with a kind of "fingers" of data along the edges, which I think is a similar result.  The end results was that EWA "looked" much better.  Even the Elliptically-Weighted-Nearest-Neighbor option, which uses the elliptical weights to pick the highest-weighted as the nearest value - without averaging the source data - was a significant improvement.  
    • I believe in the image processing world, there is a trade-off of "sharpness" and full resolution access vs. the introduction of these effects.  I.e., a kind of minor "blurring" of the image is introduced, but I don't think in practice this was very significant. I suspect the gaussian filter's reduction of aliasing effects outweigh any loss of "sharpness" in the output data.
    • The "Stalls with my dog" link above describes a metric of processing shown in the frequency domain on something called the MTF chart.  The ideal has the filter following source data up to something called the "nyquist frequency" and then sharply dropping off above that frequency.  It can be seen that e.g., Nearest-Neighbor interpolation without filtering does quite poorly on this metric, while the gaussian filter used in the EWA technique does quite well.

The algorithm itself

What follows is a very cursory pseudo-code description of the algorithm, hopefully highlighting the important aspects, and not leaving out any significant details, while not overwhelming with detail.

For each point in swath (per row, per column)
  Pre-Calculate ll2rc – lat/lon-to-row-column
  (giving floating-point row/col in target space, not integer row/col) 
For each row-set in swath (rows-per-swath)
  Compute_ewa_parameters: (ellipse parameters per column)
    For each column in row-set
      <compute ellipse parameters>
        Use values in adjacent columns for horizontal delta of ellipse calculation
        Use first row of row-set to last row of row-set, averaged over the number of rows
          for the vertical delta of ellipse calculation.
  Compute_ewa: (output values per target grid cell)
    For each row in row-set
      For each column in swath
        <assign values for recurring factors >
        <get ewa_parameters for row & column (compute_ewa_parameters, ellipse)
        <compute perimeter box for ellipse >
        For each target row in perimeter box
          For each target column in perimeter box
            If target point within ellipse
              Compute/Lookup weighting factor
              Numerator_array(target_cell)    += weighted-distance # grid_accums
              Denomitnator_array(target_cell) += weights           # grid_weights
Target_Values = Numerator_array / Denominator_array                # output_grid

The original article shows the calculation of the perimeter-box for the ellipse as follows:

EWA Performance

  • EWA should provide relatively good performance, relative to other reprojection techniques, though it remains computationally intensive to perform projection math on every point in the source grid.
  • The PyResample implementation offers a built-in DASK application that should improve performance across multi-core/multi-processor systems, without requiring a huge memory footprint.
    • EWA is an example of forward reprojection, where the source data grid is processed per cell, and with each mapping to 1 or more target cells to be processed.
    • Computationally, the biggest factor is performing the complex projection math for each source cell.
    • The processing is O(n * m)  - where n is the number of source points and m is the average size (number of cells) of the mapped bounding ellipse, typically < 24 and usually closer to 4 or 6. You may call the upper bounds on the size of m an educated guess, but it has been borne out in practice. 
    • The heavy lifting of computing the projection space of the source data (ll2rc) is O(n).  This is typically done once and reused for multiple science data variables per file.
    • In comparison, reverse projection algorithms have a similar O(n * m) load, where n is the number of target points, and m is the mapping factor to source data cells.  Also involved is an O(n * log-n) lookup factor to find related source cells.  Typically the source cells are preprocessed into an easily searched data structure (PyResample uses a K-dimension Binary Tree - KD-Tree).  The preprocessing includes the reprojection math and the results can be reused for multiple science data variables per file.
    • The two reprojection approaches likely have similar O() factors, but the additional complexity of the data structures and data search in reverse reprojection results in somewhat slower performance.  
    • Somewhat in compensation, the reverse reprojection approach provides much greater flexibility in implementing different interpolation techniques.  Almost all modern reprojection engines I believe have adopted reverse reprojection for this reason.
    • We noted this on the implementation of the Swath-Projector application.  EWA was similar to the other reprojection options (reverse reprojection), but generally always the faster choice.

“Off-label” application of EWA

  • The impact of the rows-per-swath parameter and options of rows-per-swath = 1 and rows-per-swath = 0 => all rows … .
  • Application to Geographically Gridded data, to regridding of data without reprojection, and to general reprojection of projection-gridded data
  • New modules to replace ll2rc – lldim2rc (Geographic Grids), rc2rc (Regridding, no projection math), xy2rc (Projected Grids, Double projection, Source-to-Target)

  • Application to Geographically Gridded data
      • There is a relatively direct relevancy of the EWA algorithm to the reprojection of geographically gridded data.  
      • The application of EWA in this case appears valid from a reprojection perspective.
        • For geographically gridded data we have an array of data, with correlated latitude and longitude values.  It is easy to see how the algorithm would be applied.  
        • When you look at a geographically gridded data array versus a swath data array, you can see that the geographically gridded data is generally wider than the swath, but there is no elliptical stretching of the grid cells in their geographic spacing.  The ellipse of influence for the source data is circular.  
        • There remains, however, the non-circular ellipses of influence due to the projection to a non-geographic, projected grid.  This is properly handled by the EWA implementation.
      • EWA should be a relatively efficient implementation relative to reverse projection techniques.
        • The source-cell to target-cells mapping does not have the elliptical spread of the sample-spots to consider - only the elliptical spread of the projection mapping.  There should be no more, and likely fewer cells per source cell, and thus greater efficiency per source cell count than for a swath dataset.
      • The algorithm has a gaussian filter built-in to mitigate down-sampling aliasing effects, where relevant in the output projected grid.
      • In this case, the preprocessing step of EWA - the Latitude-Longitude-to-Row-Column calculation (ll2rc) can be handled in one of two ways
        • The latitude/longitude arrays of values can be precomputed (if not directly available) and then fed into the ll2rc method
        • Alternatively, the ll2rc method can be modified into a method that directly uses the 1D dimension-scales (dimension-variables) providing latitude and longitude values.  I would call such a method llDim2rc.

  • Application to Regridding - without reprojection

      • This is a curious and perhaps less clear "off-label" application of the EWA algorithm
      • In this case the mapping of source cells to target cells is exactly circular, not elliptical.  Note however, that the EWA approach of looking at location-mapping deltas between adjacent row and column data still results in an appropriately defined "circle of influence" between the source and target grids.
      • Note also that this particular application of EWA does not care if the source/target arrays are geographically gridded or projection gridded - only that the source and target grids have the same projection.
      • Again the ll2rc method has some special handling considerations
        • There is nothing preventing the use of the first approach outlined above for application to reprojecting Geographically Gridded data - excepting for the inefficiency and processing time required.
          • I refer here to computing a pair of lat/lon datasets that can be fed into ll2rc to compute the mapping between source cells and target cells.
          • This requires projecting the source cell locations to lat/lon, and then projecting that back to the target cell locations.
          • As noted, ll2rc will work in this way but the double projection math involved is significant and ultimately unnecessary
        • Alternatively, the ll2rc method can be replaced with a method to compute the relative locations of the source and target cells using the two grid definitions and without consideration of the grid-projection involved.  This can be done producing the same data results as the ll2rc method - a source to target mapping of row-column values, floating point results, i.e., to the target row-column space.
          • I refer in this case to the grid definition as the combination of x and y projected locations of the corner points, in projected meters (or lat/lon for geographic grids); the number of rows and columns; and implicitly, the cell resolution in projected meters (degrees for geographic grids).
          • Reprojection math can be replaced with affine-matrix math, as one approach
          • I would call such a method rc2rc.
  • Application to General Reprojection
      • As for Geographically Gridded data being reprojected via the EWA algorithm, I think there is utility in apply EWA to general reprojection of projection gridded data.
      • In this case, the comparison of source data projection to target data projection results in two ellipses of influence, as was shown for the swath data projection use-case.  
      • For projection-gridded data, you can imagine the Tissot ellipse for the source data defining an ellipse of influence of the source cell to a geographic region on the earth's surface.  And, you can imagine the Tissot ellipse for the target data defining an ellipse of influence for the target cell back to a geographic region - as is the case with swath data.
      • Thus there is a strong parallel of applying EWA to projection gridded data, with two elliptical areas of influence, just as it is used for swath data.
      • In this case, there might be a larger resulting ellipse of influence, in some areas of the target output grid, than is seen with swath data.  This relative difference in application, however, I don't think affects either the validity of the results, or the relative performance of the algorithm.  Per source-cell processing might exceed that for swath data, in those regions, but such processing is appropriate and necessary for complete grid coverage.  I expect that a similar processing expansion would occur for reverse projection techniques as well, thus EWA remains competitive.
      • Re. the ll2rc method, in this case there is the necessity of both the projection of the source grid location to lat/lon values and the projection of geographic location to target grid.  Both approaches mentioned for handling Geographically located data are relevant - (A) compute lat/lon data arrays to match the source data grid, and then feed into the existing ll2rc.  Or (B) - supplement the source data location projection to the existing ll2rc implementation to create what I would call an xy2rc method.

Some general observations about reprojection quality

  • (Probably will generate a separate wiki page along side the other projection info pages mentioned above)
  • I think the main issue with projection/reprojection is the nature and extent of the "distortion"/stretch of the projected grid relative to the earth-surface, and relative to the subset area of interest if not the whole earth.  The proj library provides a distortion metric for a singular projected location. The Tissot Indicatrix provides a useful visualization of the stretch per location, and when presented on a map - across the map surface.  When reprojecting data, there is a modified set of Tissot ellipses of "distortion"/stretch across the resulting data grid.  I don't quite yet know how to characterize this for an entire grid, but I think there is a useful metric there.  This would be especially relevant for reprojection that is inappropriate beyond certain areal boundaries - not too far North/South for Mercator, not too far from the North/South Pole for Polar Stereographic, not too far from the central meridian for UTM/Transverse-Mercator, etc.
  • The second issue of concern is the potential introduction of downsizing aliasing artifacts.  Again, I'm not too sure of the metrics, but it has been shown to be visibly disconcerting in reprojection examples I've seen, and seems like a relevant concern to the scientific community.
  • I've not spoken about how this plays out between the Data Regridding Wizard and back-end services.
    • I think the Data Regridding Wizard should be supporting the model UI introduced with that feature.  It can address the two concerns I mention above, and assist in suggesting and/or evaluating interpolation options.
    • Ultimately, the back-end services should focus on providing the highest quality outputs, in an efficient process, for a given interpolation option.  There will be, I imagine, several interpolation techniques that need to be developed, for various data products.  I hope that the Data Regridding Wizard will be able to evaluate and propose good interpolation techniques, while the backend services focus on providing those different interpolation techniques.